Sifat-sifat Grup

 Akan diberikan suatu grup yaitu (G, o) dengan o adalah operasi biner. Kita harus berhati-hati bahwa lambang operasi “ o ” bukanlah semata-mata operasi komposisi (seperti pada fungsi) meski memiliki lambang yang sama dengan komposisi fungsi. Jadi “o” hanyalah pelambangan saja tentang operasi biner pada grup yang diberikan.

Teorema 1:
Elemen identitas dalam suatu grup adalah tunggal

Bukti:

 

Teorema 2

Setiap elemen dari suatu grup memiliki invers yang tunggal

 

Teorema 3

Dalil kanselasi dipertahankan atau berlaku pada suatu grup.

 

Teorema 4

 

 

Teorema 5

Misal (G, o) adalah grup. Untuk setiap a,b Î G maka persamaan a o x = b dan y o a = b memiliki selesaian yang tunggal di G 

Bukti:

 

Aksioma Pada Himpunan

Aksioma 1 (Ekstensional)
jika dua himpunan mempunyai anggota yang sama persis, maka himpunan tersebut sama.

Aksioma 2 (Himpunan Kosong)
himpunan kosong adalah himpunan yang tidak mempunyai anggota

Aksioma 3 (Pasangan Himpunan)
untuk setiap himpunan u dan v , ada himpunan yang memiliki anggota hanya u dan v, ditulis {u,v}

 
Aksioma 4 (Gabungan Himpunan)
untuk sembarang himpunan yang anggota-anggotanya adalah himpunan yang termuat disalah satu a atau b(atau keduanya)

 

 Aksioma 5

Untuk sebarang himpunan a, ada himpunan yang anggota-anggotanya hanya subset-subset dari a.

Persamaan Eksponen

Persamaan eksponen adalah persamaan yang peubahnya berfungsi sebagai eksponen
(pangkat) dari suatu bilangan berpangkat.

berikut adalah sifat-sifat dari persamaan eksponen:

beberapa bentuk dari persamaan eksponen adalah sebagai berikut:

perlu di ingat :
1. Jika dan , maka m = n.

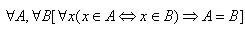
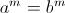2.  Jika dengan a dan b bilangan positif,   maka m = 0

Logaritma

Logaritma adalah operasi matematika yang merupakan kebalikan dari eksponen atau pemangkatan.Rumus dasar logaritma: b^c= a ditulis sebagai  (b disebut basis). Logaritma sering digunakan untuk memecahkan persamaan yang pangkatnya tidak diketahui. Turunannya mudah dicari dan karena itu logaritma sering digunakan sebagai solusi dari integral. Dalam persamaan , b dapat dicari dengan pengakaran, n dengan logaritma, dan x dengan fungsi eksponensial.

berikut adalah sifat pada logaritma:

Menyelesaikan Desimal Berulang

Kadang kita menemui masalah tentang bilangan desimal, bilangan desimal merupakan bilangan rasional(bilangan yang dapat dinyatakan dalam bentuk a/b) misalnya saja 0,5. bilangan 0,5 ini dapat dinyatakan dalam bentuk bilangan rasional yaitu: 1/ 2 = 4/ 2 = 4/ 8. namun bagimana kita mengetahui bentuk rasional pada bilangan Desimal yang dibelakang komanya(,) terdapat bilangan berulang sampai tak hingga,
contoh:
x = 0, 136136136...
untuk menyelesaikannya ikutilah langkah berikut;
kalikan masing - masing ruas dengan 10^n (n adalah banyaknya digit yang berulang setelah koma) dala hal ini adalah 10^3 karena digit yang berulang adalah 136

Sistem Bilangan Riil

Definisi bilangan Riil -------> Sekumpulan bilangan (Rasional maupun tak rasional) yang dapat mengukur panjang, bersama-sama dengan negatifnya dan nol

didalam bilangan Riil masih terdapat bermacam-macam bilangan, seperti; bilangan asli, bulat, dan rasional.
untuk lebih jelasnya lihatlah gambar dibawah ini:

Hukum-hukum pada Himpunan

definisi--->Himpunan didefinisikan sebagai kumpulan obyek-obyek yang memiliki sifat tertentu yang dapat didefinisikan dengan jelas (tegas).

Hukum-hukum pada himpunan: